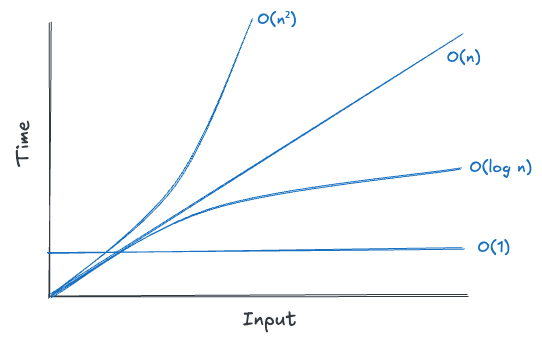
알고리즘의 스피드 표현법 - Big O 시간복잡도
알고리즘 시간 복잡도 정리
시간 복잡도란?
알고리즘의 속도는 완료까지 걸리는 절차의 수로 결정된다. 예를 들어, 10초 만에 실행되는 알고리즘과 20초 걸리는 알고리즘을 단순히 “빠르다” 또는 “느리다”로 구분하지 않는다. 같은 알고리즘이라도 컴퓨터라는 하드웨어가 속도를 결정하기 때문이다.
따라서, 같은 작업을 수행할 때 더 적은 절차를 필요로 하는 알고리즘이 효율적이다. 예를 들어, 5단계로 끝나는 알고리즘은 10단계가 필요한 알고리즘보다 효율적이다.
시간 복잡도 유형
알고리즘에서 시간 복잡도란 주어진 문제를 해결하기 위해 알고리즘이 수행하는 연산 횟수를 말한다.
- 빅-오메가(Big-Omega): 최선의 경우 연산 횟수를 나타낸 표기법
- 빅-세타(Big-Theta): 평균적인 연산 횟수를 나타낸 표기법
- 빅-오(Big-O): 최악의 경우 연산 횟수를 나타낸 표기법
최선과 최악의 경우란?
입력 데이터에 따라 알고리즘이 얼마나 많은 연산을 해야 하는지를 뜻한다.
최악의 경우는 알고리즘이 가장 많은 연산을 해야 하는 상황이다. 즉, 입력 데이터가 가장 비효율적으로 구성되어 연산이 최대한 많이 필요한 경우를 의미한다. 예를 들어, [1,2,3,4,5] 배열이 있을 때 선형탐색(for문)으로 5를 찾는 경우 5는 배열의 제일 마지막에 있기 때문에 모든 요소를 다 확인해야 한다. 이는 최악의 상황이다. 반면, 최선의 경우는 가장 적은 연산으로 문제를 해결할 수 있는 상황이다. 같은 배열에서 1을 찾는 경우, 가장 앞에 있으니 한 번에 찾을 수 있다. 이 경우 최선의 상황이라고 할 수 있다.
코딩테스트에서는 빅-오 표기법을 기준으로 수행 시간을 계산한다.
시간 복잡도 종류
O(1) (상수 시간)
1
2
const numbers = [1, 2, 3];
console.log(numbers[0]);
numbers 배열(인풋) 사이즈 크기가 10이든 100이든 1 스텝이면 코드 실행이 끝난다. 인풋이 얼마나 크든 말든 관계없이 동일한 수의 스텝이 필요하다. 이에 대한 시간복잡도는 상수 시간(constant time)이라고 한다. N이 얼마나 크든 관계없이 끝내는데 동일한 숫자의 스텝이 필요하다.
1
2
3
const numbers = [1, 2, 3];
console.log(numbers[0]);
console.log(numbers[0]);
콘솔을 두 번 출력한다고 해서 시간 복잡도가 O(2)가 되는 것은 아니다. Big O 표기법은 알고리즘의 전체적인 성능 변화(스케일링)에만 관심이 있으며, 입력 크기(N)가 커져도 연산 횟수가 고정이라면 시간 복잡도는 여전히 O(1)로 간주한다. 예를 들어, 200번의 고정된 연산이 필요한 함수도 시간 복잡도는 O(200)이 아닌 O(1)로 표현된다.
O(1) 알고리즘은 항상 선호되는 알고리즘이지만 현실적으로 항상 그렇게 만들긴 어렵다.
O(N) (선형 시간)
1
2
const numbers = [1, 2, ...100];
numbers.map(console.log); // 1 ~ 100 숫자 차례로 출력
numbers의 크기가 커지면 콘솔을 출력하는 횟수도 많아진다. 이를 시간복잡도로 나타내면 O(N)이다.
1
2
3
const numbers = [1, 2, ...100];
numbers.map(console.log);
numbers.map(console.log);
만약 이렇게 map을 두 번 호출해도 시간복잡도는 O(2N)이 아닌 O(N)이다. 상수는 무시한다.
O(N²) (이차 시간)
2차 시간은 중첩 반복이 있을 때 발생한다.
1
2
3
4
5
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length; j++) {
console.log(i, j);
}
}
이렇게 중첩으로 있다면 배열의 각 아이템에 대하여 루프를 반복하여 실행한다. 시간복잡도는 인풋의 n 가 된다. 루프 안의 루프에서 실행하니 인풋이 10개라면, 완성하는 데 100번의 스텝이 필요한거다.
O(log N) (로그 시간)
매번 스텝을 진행할 때마다 인풋의 반을 나눈다. 인풋이 2배로 커져도 한 번만 더 나누면 되니 검색을 하기 위한 스텝은 +1만 증가한다. 시간복잡도는 O(log n)이다. Big O에서는 base는 쓰지 않는다.
O(log N)은 O(1) 다음으로 효율적이며, 대량의 데이터에서도 빠르게 실행된다.
정리
- O(1): 입력 크기에 상관없이 항상 일정한 시간 내에 실행되는 가장 이상적이고 빠른 시간 복잡도
- O(log n): 입력 크기가 커져도 비교적 적은 연산 횟수로 작업을 완료할 수 있는 효율적인 시간 복잡도
- O(n): 입력 크기에 비례하여 연산 횟수가 증가하는 시간 복잡도로, 데이터 크기가 커질수록 실행 시간이 선형적으로 늘어남
- O(n²): 입력 크기에 따라 연산 횟수가 기하급수적으로 증가하는 비효율적인 시간 복잡도
참고
- 알고리즘 코딩테스트 책 (이지스퍼블리싱)